Aussie version of Eratosthenes’ diagram
In the famous diagram attributed to Eratosthenes of Alexandria showing how to find the girth of our planet, there is a well on the tropic of Cancer over which the sun shines directly down at noon on June 21st, and there is a pole at Alexandria that casts a shadow at that same moment. ..The distance between well and pole is given (800 km in modern units), etcetera.
{note: _ The diagram was meant only to illustrate the logic involved. ..It could not have been what he actually did to get his result, since he had no way of accurately measuring such a long distance. ..Clearly, Eratosthenes must have recast the problem in a way that was measurable with accuracy. <<see item: Eratosthenes: Two~pole solution on this website.}
Transposing to Australia…
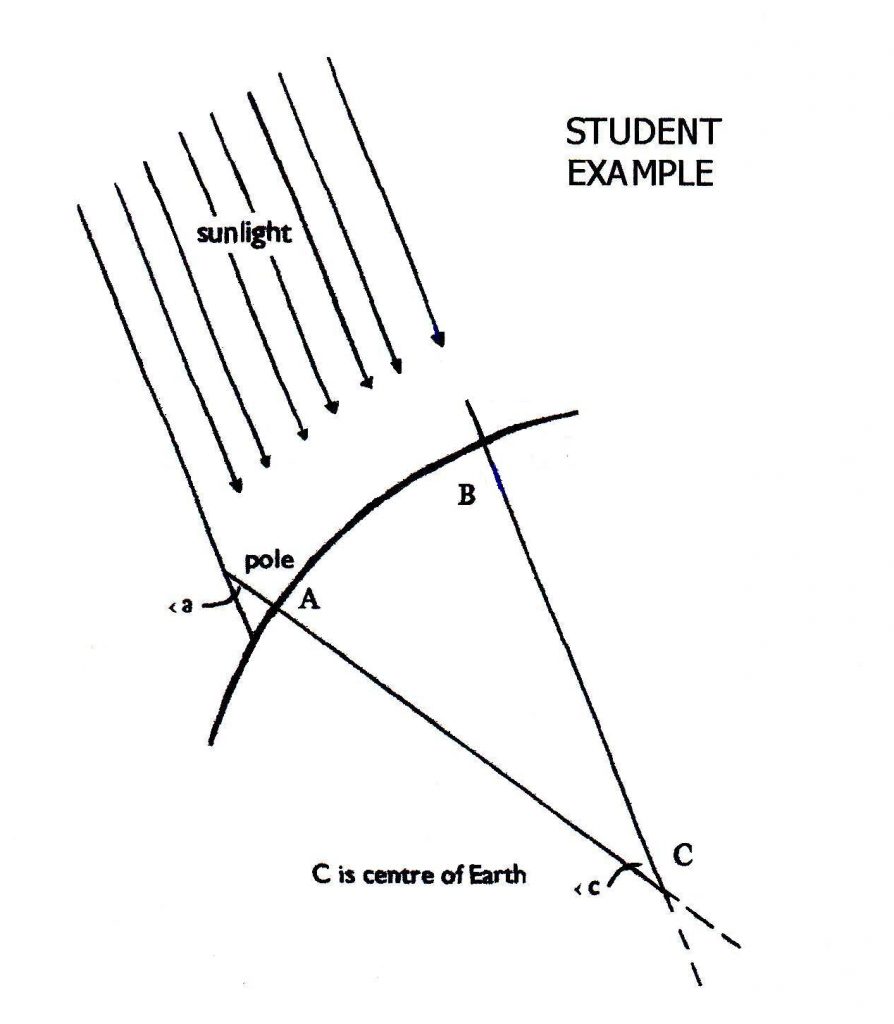
It so happens that Rockhampton QLD is on the tropic of Capricorn, while due south of it about 12oo km is Sydney NSW. ..On Dec 21st at high noon, a pole at Sydney will cast a shadow, while a pole at Rockhampton will not. (Not clock noon, but local high noon when the sun is directly overhead.)
In the diagram …Sydney is at ‘A’. …The angle at the top of the pole is labelled ‘a’ while the one at centre of Earth is ‘c’. ..Rockhampton is at ‘B’.
Eratosthenes was wanting to find the girth of Earth, something we today know is about 40,000 km. ..But the .Down Under. diagram is nonetheless useful, for it may be used to challenge students to find something else — At local noon on Dec 21st ….. for poles of different heights at Sydney, what will be the length of the shadow each pole casts?
Students can use this formula — shadow length = aH, where H is the height of the pole in metres, and_ a is 0.19. … Simple, no? … And also the reverse applies — given the length of shadow, how tall is the pole?
Students could also be required to show that parameter ‘a’ really is 0.19. …for which they may use 3.14 as the value of pi. ..Or instead, the teacher can go though the steps of how: a = 0.19 is obtained.
The key to this is recognising that the angle at the top of the pole that sunlight makes at that high~noon moment is the same as the angle at the centre of Earth extensions of the poles at Sydney and at Rockhampton would make.
Same angle, ..two arcs, ..one known, one unknown. ..The known one is 3% of its entire circle (1200 /40,000), …and the smaller will be the same %age of its circle, ..of which the pole is its radius. That smaller arc is the length of the pole’s shadow at high noon on that day. _When it is worked through, parameter a = (run/40,000) x 2pi … where run means the distance between the two poles. ..Simplified:_ a = [run x pi]/20,000
In Western Australia from the village of Southern Cross, where Newman is about 830 km due north, which is 1/48th of the Earth’s circumference, this gives a = 0.13. …It also yields a value for the Girth of Earth that is 99% accurate.
__________________________________________
In North America, the city of Mazatlan in Mexico is nearly on the tropic of Capricorn, while 950 km due north is El Paso on the border with Mexico. Parameter a will be 0.15 in this case.
Havana in Cuba is also nearly on the tropic of Capricorn and about 1300 km south of Greenville, SC ..so parameter a = 0.20
Elswehere: __ In Chile, the city of Antofagasta in very nearly on the tropic of Capricorn, while something like 1200 km due south is the city of Rancagua, so the above calculations may be used there as well. Or adjust the distance if Talca is used instead.
South Africa can also do this. _Polokwane is somewhat north of the Tropic of Capricorn, and it is about 680 km north of Pietermaritzburg which is nearly due south of it.
This website is https://regionalseats.ca/wp/