How he likely measured the girth of Earth
Eratosthenes was a learned ancient Greek who, among other things, produced a map of the then known world that stretched from India to Britain. ..Geography and geometry were two of his specialties. He lived in Alexandria and was head of its Great Repository,* which not only housed thousands upon thousands of scrolls of scholarly output, but a good many scholars as well. _Today it would be a university. In his day there were few others like it, and none more famed.
{* Usually wrongly called the Great Library. ..But a library is a collection of books. As instance, a shelf of books in someone’s abode is their personal library. ..There were no books back then.}
Something like 2250 years ago Eratosthenes produced an astonishingly good estimate of Earth’s girth. ..Exactly how he did it is unknown because the scroll of his original work was lost, likely to fires set by religious fanatics who felt the holy words of some religious sage was all the world needed in the way of wisdom.
Yet, we do know that he had such an estimate, for a simplified example survived meant for students of geometry. ..The result it provides is surprisingly good. ..This example was apparently concocted by someone else some decades later, who must have seen Eratosthenes’ scroll.
Student example
That geometry exercise was meant to demonstrate the logic involved, of how the planet’s girth could be estimated from only two things. ..One is the sunlight’s slant at Alexandria at the time it was streaming into a well near Aswan and reflecting off the water’s surface. (It only happened for a few minutes at noon on one day of the year, never mind why.) The other was the distance that well was from Alexandria.
But how could that distance be known with any accuracy at that time?
The demonstration was made very simple by also giving the students the angle at Earth’s centre. .. It was set up like this: _[i]_Beams of sunlight are parallel;_ [ii]_the Earth is a sphere; _ [iii]_the pole at Alexandria and the well at Aswan are both perpendicular to the flat surface; ..thus each points to the centre of Earth; _ [iv]_the distance between pole and well is known; and _ [v]_the angle:c at the planet’s centre is 1/50th of its circumference… Those were the givens.
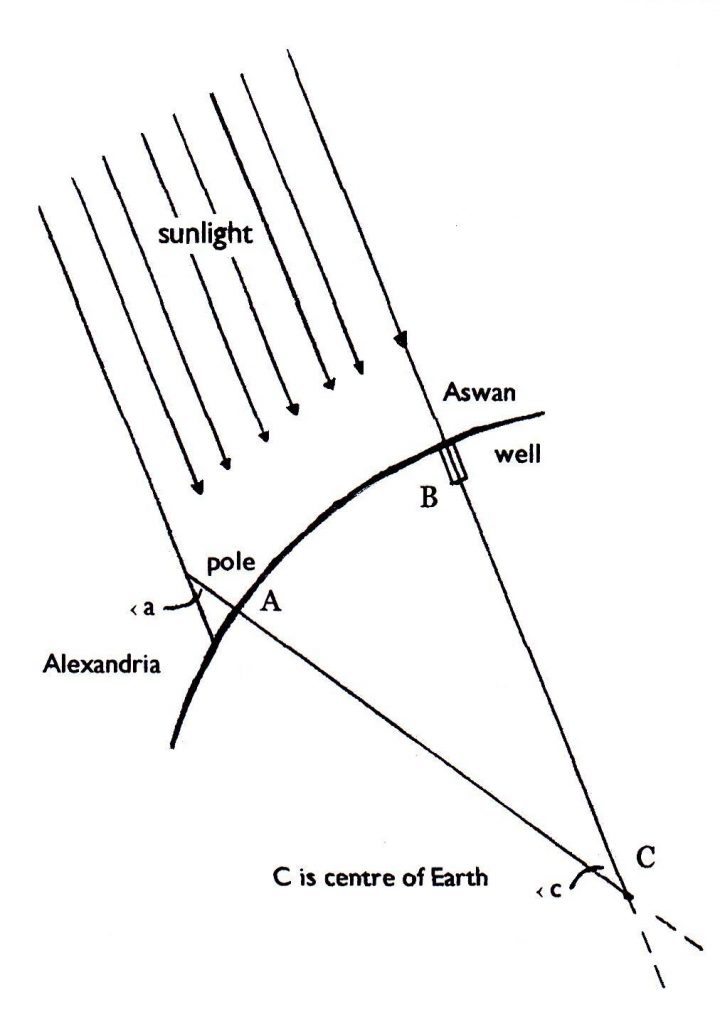
Added to the diagram here are angle:a and angle:c ..which the students can see are the same. This is because sunlight reflecting off the well’s water is aimed at the planet’s centre, ..as does the perpendicular pole.
An extended line of the pole creates angle:c ..while the pole itself creates angle:a with sunlight that is parallel to what is streaming down the well. _Two parallel lines crossing a straight line create equal angles. This becomes important shortly.
The distance they were told was 5000 stadia, which times 50 gives a girth of 250,000 stadia, ..a truly mind boggling distance for those students.
Now the unit of measure that Eratosthenes used was the stadium, an actual building. ..Those ancient Greeks were very literal and the stadium in question would have been the one at Alexandria, rather than the one closer to Athens, which of course those living there used.
It is said the stadium at Alexandria was about 157.5 metres long, so 5000 such would run to 39,375 km. ..This is within 2% of today’s accepted figure for the mean girth of our planet.
Eratosthenes actual calculated figure would have been somewhat different than 5000 stadia, though likely not greatly different. ..Perhaps it was more accurate, perhaps not — we simply don’t know.
Today’s equivalent of that student problem is 800 km times 50 for a girth of 40,000 km. ..(Well it would be, since that is how the devisors of the metric system came up with the distance of a kilometre: 40,000 of them equalling Earth’s girth.)
<< Here is something else of interest — because on the solstice day the sun is directly overhead anywhere along the Tropic of Cancer, it follows that two places an equal distance from the tropic.. one on each side of it.. for the same height of pole will cast the same length of shadow, though opposite in direction. __Here a good example is Port Said to the north and Omdurman to the south, in Sudan. ..Each is about 870 km from the tropic.>>
What he likely did
What did he do? ..The student exercise provides the logic, but Eratosthenes could not have measured a distance of 800 km with much accuracy, and he would not have just guessed at it.
Clearly, he must have set the problem in a way where the distances were measurable. ..So let’s approach the problem as he likely did, using the plane geometry schoolchildren still learn.
Intermediate between the well near Aswan and the pole at Alexandria, place a second perpendicular pole and ignore the well. ..This complicates things somewhat. ..As both poles will cast shadows, taking measurements at noon on or near the longest day of the year in June should serve:
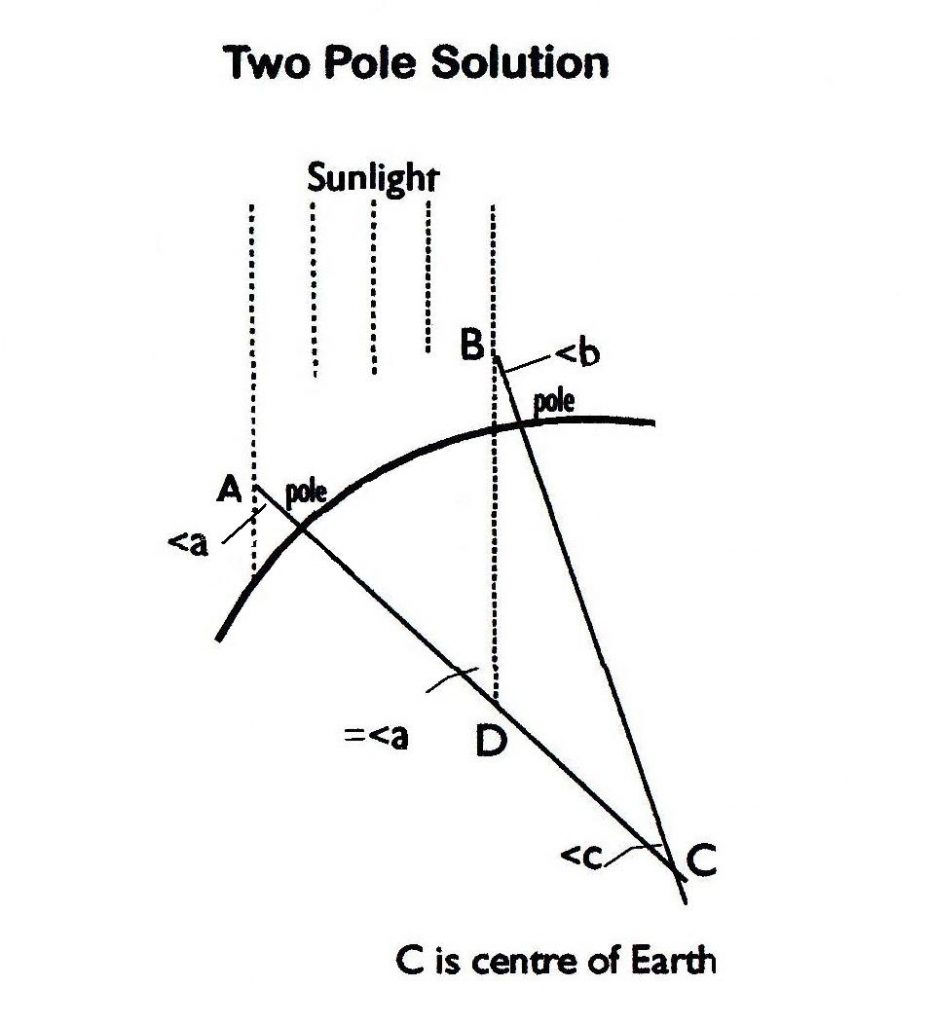
First, notice the triangle BDC whose three angles make 180 degrees. ..One of those is at D, where it plus its companion angle also make 180 degrees, so that companion angle must equal (angle:b + angle:c). ..That companion angle also equals angle:a.
So with: (b + c) = a _it then follows that c = a – b, which means the difference between the angles at the top of the poles is the angle that extensions of the poles would make at the centre of Earth.
What we know now …
On the diagram above the radius of Earth is the distance from C to the base of either pole. Eratosthenes knew that twice pi times the radius would be Earth’s girth. So he had to find what that radius was.
Of course, we know today that Earth’s girth is ~40,000 kilometres, and dividing by twice pi gives us that Radius.
What we don’t know is what Eratosthenes very carefully measured. ..As he lived in Alexandria, the more northern pole would have been near there, and the other pole due south of it, so they would both be on a Great Circle whose centre would be the centre of the planet.
Eratosthenes needed an accurate measure of distance between the two poles and also at each the length of shadow strictly horizontal to the pole cast from the same height on each pole at noon of the solstice day. (Or the next day wouldn’t make much difference.)
{_note: the ‘poles’ may have been very tall rods. ..Also, likely a trusted slave or student did the actual measuring. ..Why would this important scholar want to be out in the desert in the midday sun!}
It is said he took advantage of a survey underway to lay out the boundaries of new fields to be irrigated from wells newly dug. ..And he was able to use those surveyors to measure out a straight north-south line of some distance, at each end of which a pole would be erected. ..He could do it because Eratosthenes was a man of great importance, head of the Great Repository and also tutor to the ruler’s sons. So this tale is certainly plausible.
Whatever the actual distance was, for convenience we can say they were 40 km apart. ..Now, let’s consider those shadows. ..Because we don’t know where the poles were, we don’t know what the sunlight’s slant was at either of them. ..So we can’t estimate the length of either shadow.
Eratosthenes had those measurements done very carefully. And what did that give him?
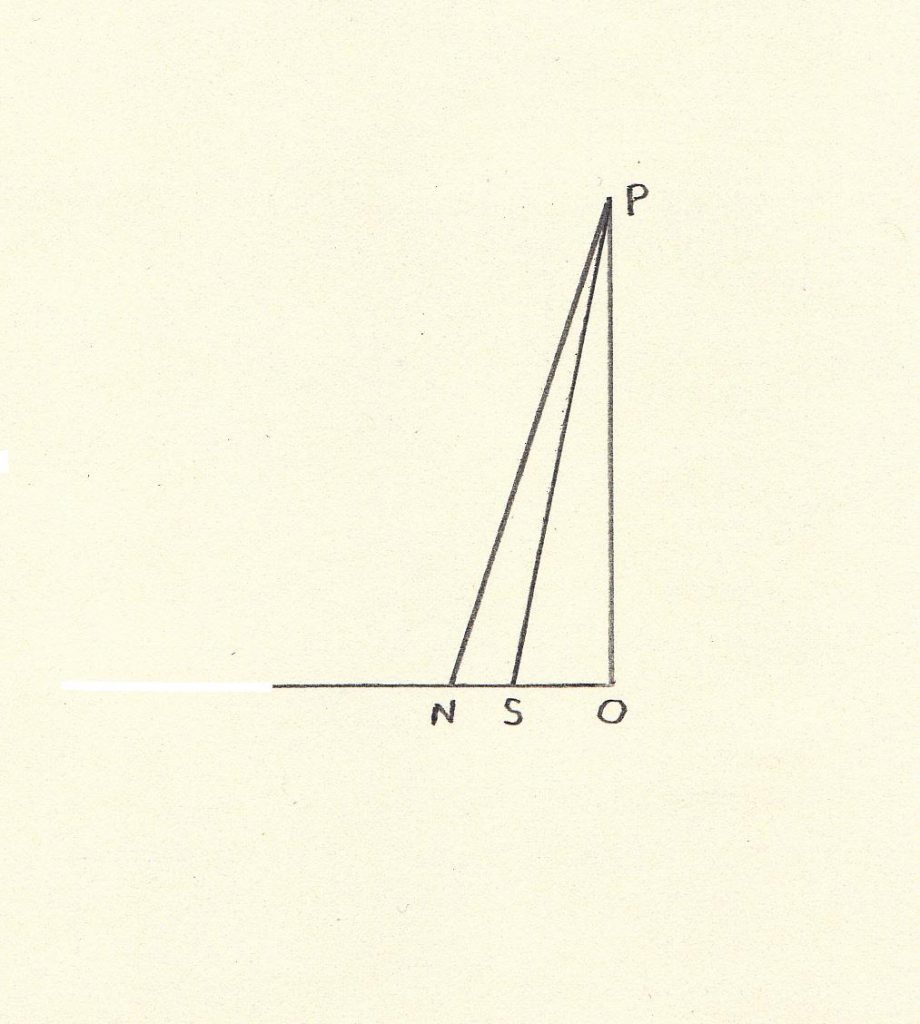
Here, O-S is the length of shadow at the southern pole, O-N the length of shadow at the northern one, ..with OP the same height on the poles that was used to produce the shadows. ..Angle:c is the angle at P between the S and N lines. ..And (N-S) is the the arc of that angle for a circle whose radius is the height on the pole.
By this time Archimedes [the best geometer then] had a value for what we today call pi, and Eratosthenes would have known of it. ..It is the value of a circle’s circumference over its diameter, which Archimedes said was about 22/7. __So if he wanted to, Eratosthenes could calculate the circumference of a small circle whose diameter is twice the height of the pole. ..But let’s look at this more generally:
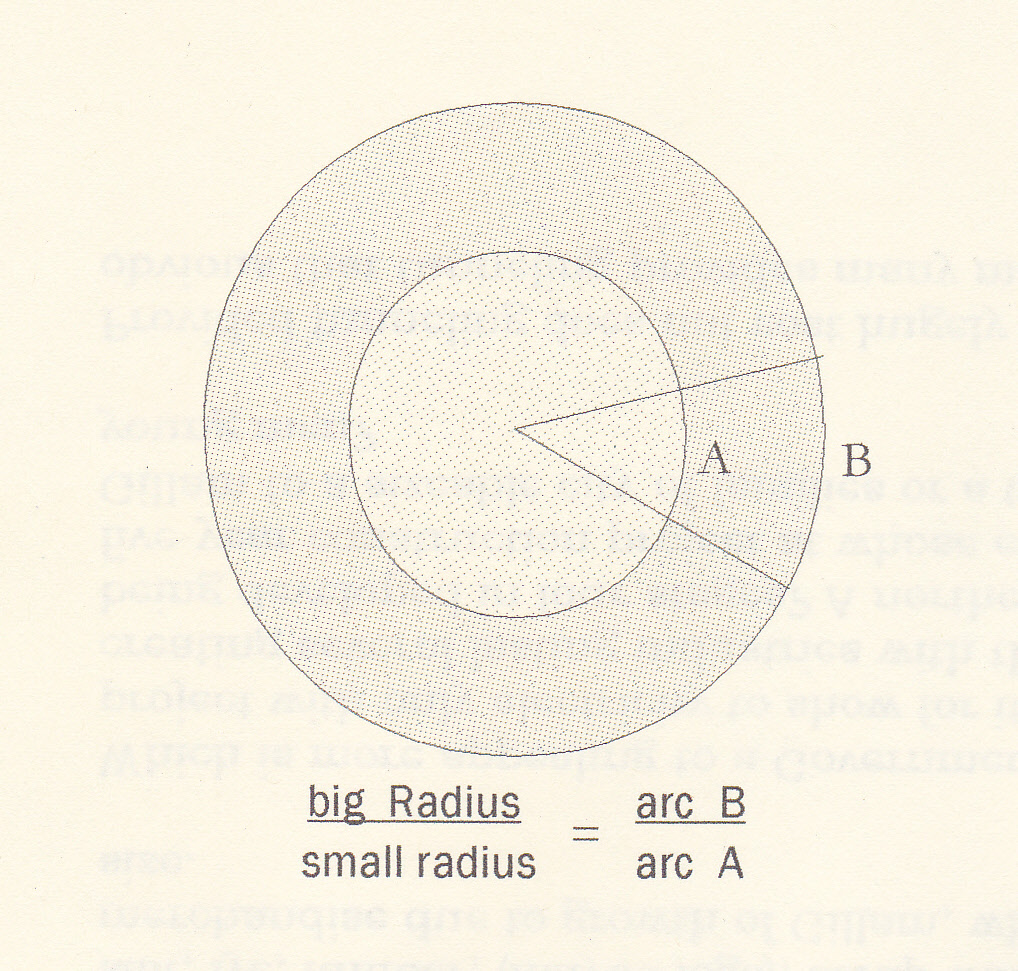
For any concentric circles with a common angle at the centre of them, the ratio of their radiuses is also the ratio of the two arcs (here B/A) made by that angle. ..As can be seen, the big Radius is equal to: (arc B / arc A) times the small radius. [Yes, I know the plural is radii.]
Eratosthenes had an uncommonly huge circle (Earth) and a much more modest one, whose radius was the height of the pole. ..So the ratio he needed was simply the large arc — (the distance between the two poles) — over the small arc — (the difference in the lengths of the shadows). ..which have in common angle:c. ..From these he could get the size of Earth’s radius. Then two pi times it yields the Girth of Earth.
An Interesting Challenge for today
Since we already know Earth’s girth is ~40,000 km, then the given arc of 40 km is 0.001 of the total girth. .. Also, since the small circle and the huge one have the same centre angle in common, ..it means the arc of that angle must be 0.001 of the small circle’s circumference.
The Challenge — Find the length of the small arc, without using a calculator!
Numerical example*
- Say the difference in shadow lengths is 3.2 cm;
- The height of the pole is 5.0 m;
- The distance between the poles is 40.0 km.
The ratio of the arcs is 40,000 m / 0.032 m _(which also is 10,000/0.008) _ and that = 1,250,000. So, that ratio times the small radius of 5 m gives Earth’s radius as 6,250 km. __And 2 pi times it is the Girth, which here is 39,270 km.
Alternatively, we could first calculate the circumference of the small circle, and then take the ratio times it to get Earth’s girth.
[* However, it is more likely he used dividers to obtain the number of small arc lengths which fit into a section of the large arc, and so avoided numerical calculation as much as possible, given the awkwardness of the number system available to him then.] __[Jan 2022 … Likely he had an abacus to aid in numerical calculations.]
Challenge answer …. Circumference of the small circle is 2pi times its radius of 5m, … which is 10pi metres. … And 0.001 times that is 10pi mm …so with pi = 3.1416, that small arc is 31.416 mm …31.4 mm approximately.
… from the website — regionalseats.ca/wp/